Matemáticas Discretas y Algorítmica

Clase del 27 de Julio de 2011

Para el tema de Compuertas Lógicas dirígase a la presentación en apuntes de clase...

Ver documento EJEMPLO en la sección de Apuntes de Clase...

El algoritmo de Floyd-Warshall compara todos los posibles caminos a través del grafo entre cada par de vértices. El algoritmo es capaz de hacer esto con sólo

V 3

comparaciones (esto es notable considerando que puede haber hasta

V 2

aristas en el grafo, y que cada combinación de aristas se prueba). Lo hace mejorando paulatinamente una estimación del camino más corto entre dos vértices, hasta que se sabe que la estimación es óptima.
Sea un grafo

G

con conjunto de vértices

V

, numerados de 1 a N. Sea además una función

caminoMinimo(i, j, k)

que devuelve el camino mínimo de

i

j

usando únicamente los vértices de 1 a

k

como puntos intermedios en el camino. Ahora, dada esta función, nuestro objetivo es encontrar el camino mínimo desde cada

i

a cada

j

usando únicamente los vértices de 1 hasta

k + 1

.
Hay dos candidatos para este camino: un camino mínimo, que utiliza únicamente los vértices del conjunto

(1... k)

; o bien existe un camino que va desde

i

hasta

k + 1

, después de

k + 1

hasta

j

que es mejor. Sabemos que el camino óptimo de

i

j

que únicamente utiliza los vértices de 1 hasta

k

está definido por

caminoMinimo(i, j, k)

, y está claro que si hubiera un camino mejor de

i

k + 1

j

, la longitud de este camino sería la concatenación del camino mínimo de

i

k + 1

(utilizando vértices de

(1... k)

) y el camino mínimo de

k + 1

j

(que también utiliza los vértices en

(1... k)

).

Por lo tanto, podemos definir

c a m i n o M i n i m o (i, j, k)

de forma recursiva:
$\textrm{caminoMinimo}(i,j,k) = \min(\textrm{caminoMinimo}(i,j,k-1),\textrm{caminoMinimo}(i,k,k-1)\,+\,\textrm{caminoMinimo}(k,j,k-1));\,\!$
$\textrm{caminoMinimo}(i,j,0) = \textrm{pesoArista}(i,j);\,\!$
Esta fórmula es la base del algoritmo Floyd-Warshall. Funciona ejecutando primero

c a m i n o M i n i m o (i, j,1)

para todos los pares

(i, j)

, usándolos para después hallar

c a m i n o M i n i m o (i, j,2)

para todos los pares

(i, j)

... Este proceso continúa hasta que

k = n

, y habremos encontrado el camino más corto para todos los pares de vértices

(i, j)

usando algún vértice intermedio.

Matriz Inversa por Determinantes

Cálculo de la matriz inversa pór determinantes

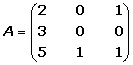
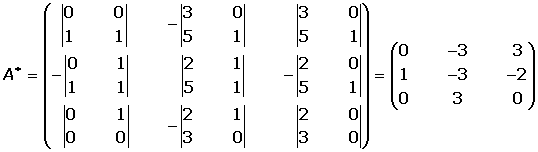
Ejemplo

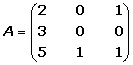
1. Calculamos el determinante de la matriz, en el caso que el determinante sea nulo la matriz no tendrá inversa.

2. Hallamos la matriz adjunta, que es aquella en la que cada elemento se sustituye por su adjunto.

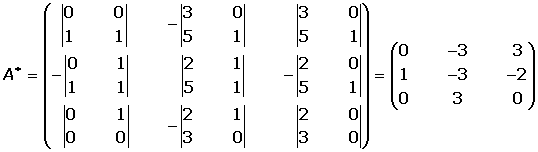
3. Calculamos la traspuesta de la matriz adjunta.

4. La matriz inversa es igual al inverso del valor de su determinante por la matriz traspuesta de la adjunta.

Transpuesta de una Matriz por Cofactores

Clase del 13 de Julio de 2011

Favor de ver los documentos anexos en sección "Apuntes de clase..." ----->

Matriz Inversa por el

Método de Gauss-Jordan

AX=Y matriz aumentada.

Solo son invertibles para sistemas cuadrados.

Sea A = (ai j ) una matriz cuadrada de coeficientes orden n. Para calcular la matriz inversa de A, que denotaremos como A-1, seguiremos los siguientes pasos:

Paso 1. Construir la matriz n ´ 2n M = (A I ) esto es, A está en la mitad izquierda de M y la matriz identidad I en la derecha.

Paso 2. Se deja tal y como está la primera fila de M, y debajo del primer término de la diagonal principal, a11, que llamaremos pivote, ponemos ceros. Luego se opera como se indica en el siguiente ejemplo.

Ejemplo:

Consideremos una matriz 3 ´ 3 arbitraria

Paso 1.

Paso 2.

Ejemplo:

Supongamos que queremos encontrar la inversa de

La mitad izquierda de M está en forma triangular, por consiguiente, A es invertible. Si hubiera quedado toda una fila con ceros en la mitad A de M, la operación habría terminado (A no es invertible). A continuación, cogemos como pivote a33, ponemos ceros encima de éste y seguimos operando hasta que nos quede una matriz diagonal.

La matriz que ha quedado en la mitad derecha de M es precisamente la matriz inversa de A:

Para comprobar si el resultado es correcto, se procede a multiplicar AA-1, teniendo que dar como resultado la matriz identidad I.

por

Unidad 1.- Lógica Cuantificacional - 01/06/11

LÓGICA CUANTIFICACIONAL

Se hace una afirmación en el sentido que un objeto o conjunto de objetos tienen una determinada propiedad o característica.

Término:

· Sujeto: a la palabra o palabras con las que se refiere uno a un objeto.

· Predicado: es la propiedad o característica que se afirma del sujeto en una proposición.

Proposiciones:

· Singulares: es cuando el predicado se afirma de un objeto o sujeto individual, ya sea persona, país, etc.

· Universales: es cuando el predicado se dice de todos los objetos de un conjunto, ya sea estos personas, cosas concretas, abstráctos, etc.

· Particulares: es cuando el predicado se aplica aparte de los objetos que componen un conjunto

En el lenguaje natural se utilizan constantemente las proposiciones singulares, universales y particulares, no solo afirmando, sino también negando.

SÍMBOLOS DE LOS CUANTIFICADORES

1. Las letras mayúsculas A, B, C, …hasta Z se utilizan para representar los predicados y se les llama letras predicativas

2. Las letras minúsculas a, b, c …hasta w, se utilizan para representar a individuos particulares y se les llama constantes individuales.

3. Las letras minúsculas x, y, y z, se utilizan para representar a cualquier individuo y se llaman variables individuales.

4. El símbolo A invertida " símbolo que es el cuantificador universal y se lee "para todo" "para alguno". ~" invertida (ninguno)

5. El símbolo $ significa existe y se llama cuantificador existencial.

Ejemplos:

· 4 es par à Pc Þ se lee c es P

· El hidrógeno es un gas à Gh Þ se lee h es G

· 7 no es par à ~Ps Þ se lee s no es P

· El aluminio no es un gas à ~Ga Þ se lee a no es G

Su forma general es Px (proposición singular afirmativa)

Venus tiene atmósfera, à Av

Jupiter tiene atmósfera, à Aj

Tierra tiene atmósfera à At

Para toda x; si x es un planeta entonces tiene atmósfera

("x) (Px à Ax)

Todos los gordos son simpáticos

("x) (Gx à Sx)

Ningún niño es malo

("x) (Nx à Mx)

Ningún molusco es vertebrado

("x) (Mx à ~Vx)

Existe al menos una x tal que x es elemento es radiactivo

($x) (Ex ^ Rx)

Algunos elementos no son radiactivos

($x) (Ex ^ ¬Rx)

Algunos vertebrados son aves

($x) (Vx ^ Ax)

Algunos vertebrados no son aves

($x) (Vx ^ ¬Ax)

Ningún insecto es vertebrado

("x) (Ix à ¬Vx)

Todos los hombres son vertebrados

("x) (Hx à Vx)

Cuadro de oposición de las proposiciones

El cuadro de oposición de las proposiciones referido a las proposiciones universales y la las particulares

Se utilizan las letras:

A à Universales afirmativas

E à Universales negativas

I à Particulares afirmativas

O à Particulares negativas

CUADRO DE OPOSICIÓN DE LAS PROPOSICIONES

Proposiciones contradictorias, dos proposiciones contradictorias entre sí, significan que no pueden ser simultáneamente verdaderas ni tampoco simultáneamente falsas; necesariamente una es verdadera y una es falsa.

Ejemplo:

Contrarias à todos los hombres son infieles algunos hombres son infieles

Contradictoria à ninguna suegra es mala,

Dos proposiciones contrarias no pueden ser simultáneamente verdaderas, aunque si pueden ser simultáneamente falsas.

Contrarias:

A à verdadera à E es falsa

Todos los mamíferos son vertebrados à ningún mamífero es vertebrado.

E à verdadera à A es falsa

Ningún molusco es vertebrado à todos los moluscos son vertebrados

A à falsa E puede ser falsa o verdadera

Todos los hombres son mentirosos, à ningún hombre es mentiroso

Todos los hombres son invertebrados, à ningún hombre es invertebrado

E à falsa, A puede ser falsa o verdadera

Ningún elemento es gaseoso à todos los elementos son gaseosos

Ningún elemento tiene valencia à todos los elementos tienen valencia

Subcontrarias: no pueden ser simultáneamente falsas pero si simultáneamente verdaderas

Argumentos en la Lógica Cuantificacional

1.- Ley de Ejemplificación Universal (EU)

Para toda x si x es p, entonces a es p ("x)Px

Todas las estrellas brillan con luz propia ("x) (Ex à Bx)

Sirio es una estrella Es

Sirio brilla con luz propia Bs puede queda Es à Bs

Todas las repúblicas soviéticas son repúblicas socialistas

Todas las repúblicas socialistas tiene economía centralizada

Ucrania es una república soviética

Ucrania tiene economía centralizada

("x) (Rx à Sx)

("x) (Sx à Cx)

Ru àSu (1, EU)

Su à Cu (2, EU)

Ru à Cu (4, 5, sh)

Su (3, 6 mpp)

2.- Ley de Generalización Universal (GU)

("x)Px

Ningún reptil tiene sangre caliente

Todas las víboras son reptiles

Ninguna víbora tiene sangre caliente

Procedimiento general para probar formalmente la validez de argumentos que contienen proposiciones universales o particulares.

Se eliminan los cuantificadores universales

Se aplican las leyes de equivalencia e implicación correspondientes

Se añaden los cuantificadores necesarios

("x) (Rx à ¬Sx)

("x) (Vx à Rx)

Ra à ¬Sa (1, EU)

Va à Ra (2, EU)

Va à ¬Sa (3, 4, Sh)

("x) (Vx à ¬Sx) (5, GU)

Todos los mexicanos son americanos

Ningún americano es europeo

Todos los sonorenses son mexicanos

Ningún sonorense es europeo

("x) (Mx à Ax)

("x) (Ax à ¬Ex)

("x) (Sx à Mx)

Ma à Aa (1, EU)

Aa à ¬Ea (2, EU)

Sa à Ma (3, EU)

Ma à ¬Ea (4, 5 Sh)

Sa à ¬Ea (6, 7 Sh)

("x) (Sx à ¬Ex) (8 EU)

3.- Ley de Ejemplificación Existencial (EE)

($x)Px

Todos los dictadores son ególatras

Algunos dictadores son generales

Algunos generales son ególatras

("x) (Dx àEx)

($x) (Dx à Gx)

Da à Ea (1, EU)

Da ^ Ga (2, EE)

Da (4, simp)

Ea (3, 5 mpp)

Ga (4, simp)

Ga ^ Ea (6, 7, conj)

($x) (Gx ^ Ex) (8,EE)

4.- Ley de Generalización Extensial (GE)